KNN(k近傍法)とk-means(k平均法)は名前が似ているため、混同されがちです。KNNもk-meansもグループ分けのために行うのですが、KNNが教師あり学習であることに対して、k-means法は教師なし学習です。教師ありとなしの違いは、正解ラベル(正解データ)があるかないかとなります。教師あり・教師なし学習に関しても以前解説した記事がありますので、下記より参照ください。
まずはKNNとk-meansの概要について説明し、その後Pythonによる実装コード例を紹介します。
目次
KNN(K近傍法)とは?
KNN(k-nearest neighbor)はK近傍法ともよばれる機械学習アルゴリズムです。アルゴリズムとしては非常に単純であり、「近くにあるデータは似ているはずだ」という発想に基づいています。
K近傍法のKは近くにあるデータをK個集めるという意味で、多数決により分類を決定します。下図において、中央の●のデータの分類を予測したいとします。
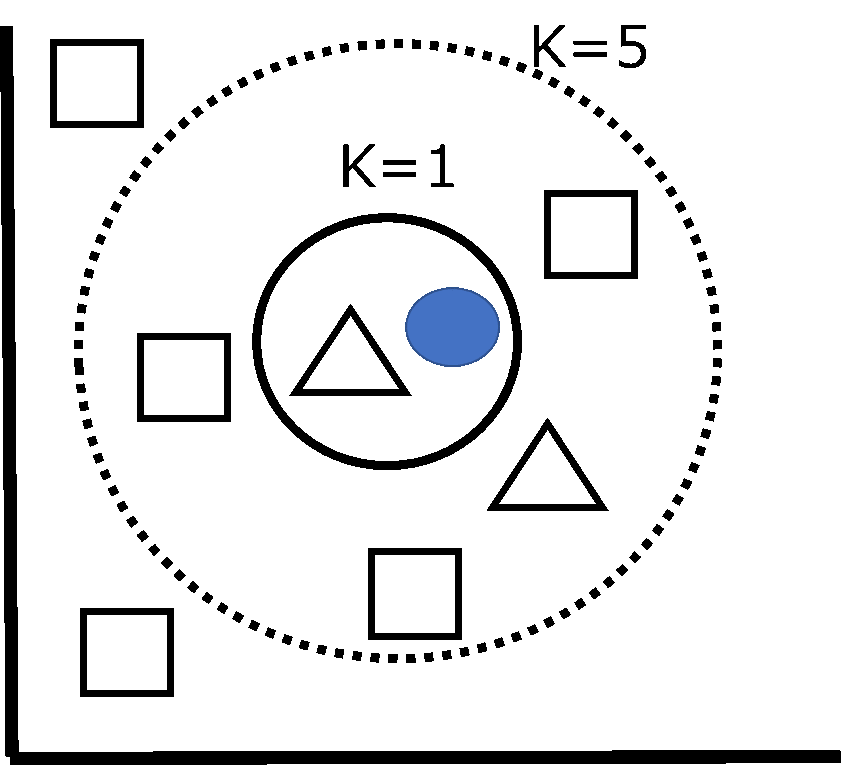
K=1のとき、近くにあるデータは△なので、●を△と予測します。K=5のとき、△は2個で□は3個です。したがって●を□と分類します。Kは人間が設定すべき変数であり、これをハイパーパラメータといいます。
KNNの他のアルゴリズムにはない特徴
一般に、AIの作成の際には、学習に時間がかかる反面、予測は一瞬で終わります。しかし、KNNでは、予測時に各データへの距離計算を行う点に注意する必要があります。予測の際に計算を実行するということで、これがKNNの他のアルゴリズムとの大きな違いとなります。
次元の呪いというKNNの弱点
また、データを予測するための特徴量の数が多くなると、KNNの精度が悪くなるという問題があります。これは次元の呪いと呼ばれるものです。
次元の呪いとは、特徴量の数(次元の数)が多くなるほど、機械学習で取り扱う問題の難易度が上がる現象です。大きく2つの困難があります。
まず1つ目の困難は、計算量の増加です。特徴量が増えるほどに計算量は増大します。ときに指数関数的に計算量が増えるため、現実的な時間内に計算が終わらないこともあります。そういう場合には、単純なアルゴリズムを使用することや、次元削減などの手段を用います。
2つ目の困難は、高次元空間においては、私たちの空間的直感が通用しないことです。なんと、高次元空間では「すべてのデータの距離が近くなる」という信じがたい現象が起きます。私たちは縦・横・高さ・時間という4次元空間内に存在していますよね(4次元ということに関して異論はあります)。「すべてのデータの距離が近くなる」とはどういうことかというと、高次元空間では、ある1点があったとしてその点に「最も遠い点と最も近い点までの距離がほぼ同じ」になるのです。つまり、高次元空間においては、最も近い点も最も遠い点も同じようなところに集まってしまいます。
そのため、特徴量の数が多くなると、距離をベースとするKNNの精度が悪くなるということを理解できると思います。一般に、何かと何かが似ているという類似度を判断するために、「データ同士の距離」を用いることが多いです。ところが次元の数が多くなると、距離を用いて類似度を判定することにはリスクがあることになります。
それでもKNNは使える
次元削減などで次元の呪いを回避できるため、KNN自体は単純ながら非常によく用いられるアルゴリズムです。
PythonによるKNNの実装
今回はscikit-learn内にあるワインの品質判定に関するデータセットを利用します。アルコール濃度やポリフェノール量などのワインの属性データと専門家による品質評価(正解ラベル)のデータです。専門家の判定を模倣するAIを作成します。
K近傍法のKは近くにあるデータをK個集めるという意味で、多数決により分類を決定するとさきほど述べました。このKは人間が設定するハイパーパラメータであり、最適なKも合わせて調べようと思います。ワインのデータはサンプル数(データの数)が178個で、専門家のワイン評価は3段階あります。したがって、調べるkとしては1から60(180÷3)までを調べます。また、標準化という属性データの単位を揃える前処理を行った上でトレーニングを行います。
#必要なモジュールをインポート
from sklearn.neighbors import KNeighborsClassifier
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import load_wine
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
import matplotlib.pyplot as plt
#scikit-learn内にあるワインの品質判定用データセットをwineという変数に代入。
wine = load_wine()
#Xにワインの特徴量を代入。特徴量は、ここではアルコール濃度や色などwineの属性データのこと。
X=wine.data
#yにワインの目的変数を代入。目的変数は、ここでは専門家によるワインの品質評価結果のこと。
y=wine.target
#トレーニングデータとテストデータに分割。
#トレーニングデータで学習を行い、テストデータでAIが実際に使えるかの精度検証。テストデータは全体の3割に設定。
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)
#標準化を実行するためのStandardScalerをインスタンス化(実体化)。fitで訓練データを標準化する際の準備。
scaler = StandardScaler()
scaler.fit(X_train)
#図示するための準備。横軸にk、縦軸にそのときの一致率
list_k =[]
list_ac = []
#KNNのkはハイパーパラメータであり、最適なKを1から60の範囲で調査
for k in range(1,60):
clf = KNeighborsClassifier(n_neighbors=k)
#transformで標準化を実際に行い、そのデータに対してサポートベクターマシンによる学習を行う
clf.fit(scaler.transform(X_train), y_train)
#テストデータにも標準化を実行し、predict(予測)を行う
y_pred = clf.predict(scaler.transform(X_test))
#正解率の算出。予測データと正解データを比較してKNNの精度検証を行う。
accuracy = accuracy_score(y_test,y_pred)
#各kとそのときの正解率をリストに追加。後で図示のために利用。
list_k.append(k)
list_ac.append(accuracy)
#簡易的な図示
fig = plt.figure()
ax = fig.add_subplot(1,1,1)
ax.set_title("正解率の推移")
ax.set_xlabel("k")
ax.set_ylabel("正解率")
ax.plot(list_k, list_ac)
# 正解率が最大となるインデックスを求める.enumerateはインデックスと値のセット。
# iがインデックスでxが正解率。xが最大のときのインデックスのリスト。
maxIndex = [i for i, x in enumerate(list_ac) if x == max(list_ac)]
#maxIndexはkより1小さいため、maxIndexの各要素に1を加える
max_k = list(map(lambda x: x+1, maxIndex))
print(max_k)
#正解率が最大となるkは[5, 7, 8, 9, 10, 11, 13, 15, 16, 17, 18, 19]
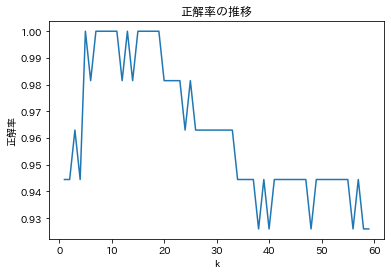
ということで、正解率が最大の100%になるkは5~19の範囲でした。したがって、k=5とk=19の間を取ってk=11くらいにすると良さそうですね。
k-menas法(k平均法)とは?
k-means法は、教師なし学習によるグループ分けの手法でした。教師なし学習でグループ分けを行うことを「クラスタリング」または「クラスター分析」と呼びます。
クラスタリングは、属性データの特徴から似たグループに分けることです。非常に単純な例をあげると、人間を身長と体重という2つの属性データから4つのグループに分ける、ような具合です。この「身長と体重のデータから、4つに分ける」という作業をk-meansに行わせるのです。
さきほどのワインの例で言うと、専門家の品質評価という正解ラベル(正解データ)を使わず、ワインの属性データだけからグループ分けを行います。
k-means法の仕組み
k-means法は、自分の好きなk個のクラスター(グループ)に分けることができます。このkは、コンピューターではなく人間が自分で設定する数字(ハイパーパラメータ)になります。k-means法の仕組みは以下のようになります。
①各データのグループをランダムに割り当てる
②グループごとに重心(各データの平均値。クラスターの代表となる点)を求める
③データに最も近い重心のグループを、再度そのデータのグループとして割り当てる
④再びグループごとの重心を求める
⑤データに最も近い重心のグループを、再度そのデータのグループとして割り当てる
・・・
これを繰り返すと、重心の位置とデータのグループ分類が変わらなくなるので、そこで終了となります。このようにしてk個のグループを求めます。
k-means法以外にもあるクラスタリング手法
k-meansの場合、分析者自身が適切なグループ数kを設定しないといけないのですが、自分でkを決める必要がないDBSCAN(Density-based spatial clustering of applications with noise)というデータの集まり具合(密度)に着目したクラスタリング手法があります。
そのほかにも、すべてのデータがバラバラの状態から徐々に似たデータ・グループをまとめていく凝集型階層クラスタリングや、データの連結性に注目するスペクトラルクラスタリング、複数の正規分布からデータが発生していると考えるGMMなどがあります。
PythonによるK-meansの実装
教師なし学習であるため、正解データである専門家の評価を使用せず、ワインの属性データだけを利用してクラスタリングを実行します。今回は3クラスに分類するとわかっているので、人間が設定する数値であるハイパーパラメータのグループ数は3で学習を行います。つまり3つのグループに分けます。
#必要なモジュールをインポート from sklearn.cluster import KMeans from sklearn.preprocessing import StandardScaler from sklearn.datasets import load_wine from sklearn.metrics import accuracy_score #scikit-learn内にあるワインの品質判定用データセットをwineという変数に代入。 wine = load_wine() #Xにワインの特徴量を代入。特徴量は、ここではアルコール濃度や色などwineの属性データのこと。 X=wine.data #yにワインの目的変数を代入。目的変数は、ここでは専門家によるワインの品質評価結果のこと。 y=wine.target #標準化を実行するためのStandardScalerをインスタンス化(実体化)。fitで訓練データを標準化する際の準備。 scaler = StandardScaler() scaler.fit(X) # データを標準化し、3つのグループに分ける kmeans_c = KMeans(n_clusters=3, random_state=0).fit(scaler.transform(X)) # 分類結果のラベルを取得する label = kmeans_c.labels_ # 一致率(正解率)を算出 accuracy_score(y,label) # 約97%の正解率
正解率は約97%となりました。実は、k-meansによるグループ分けした後のラベル(コード内のlabel)と正解データである専門家評価(コード内のy)が以下のような形になっているので、たまたまaccuracy_score(y,label)で簡単に正解率を出すことができました。やはりk-meansでもしっかりとグループ分けを行うことができました。

ただ、今回は正解ラベルのあるデータであえて教師なし学習を行いました。k-measは正解ラベルがないときに利用するものなので、正解ラベルがある場合は教師あり学習を行うのが無難です。
まとめ
ここまでKNNとk-meansの違いとPythonによるコード例を紹介してきました。長文となりましたが、最後まで読んでいただきありがとうございました。またお会いしましょう!