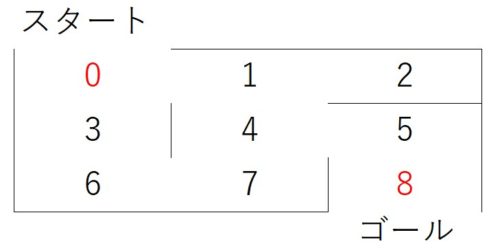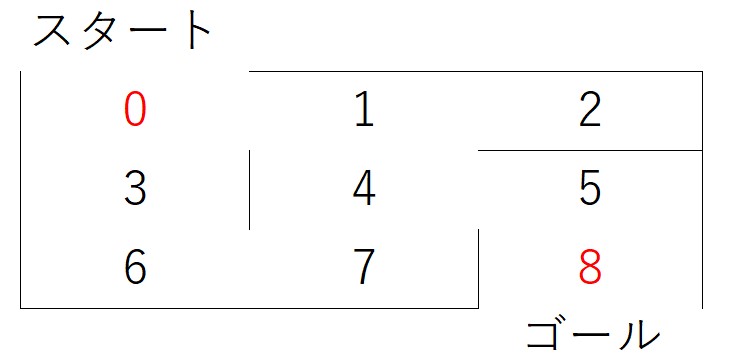
機械学習には、主として教師あり学習、教師なし学習、そして強化学習の3つがあります。このうち、教師あり学習と教師なし学習は理解しやすくPythonによるプログラミングも簡単です。一方、強化学習は理解が難しくPythonによる簡単な実装例すらなかなか見つからない状況です。この記事では、そんな強化学習をわかりやすく説明し、シンプルなプログラミングコードにより迷路の最短ルートを導くAIを作成します。今回提示するコードを拡張すれば、難解な迷路も解けるようになります。迷路を解くことにどういう意味があるのかと思われるでしょう。迷路の最短ルートがわかるということは、最短ルートで移動するロボットの頭脳AIを作成できるということです。
また、教師あり学習と教師なし学習に関しては以下の記事で解説とPythonによる実装例を紹介しています。興味がある方はそちらもぜひご参照ください。
目次
強化学習により実現できることの具体例
強化学習で何ができるようになるかというと、その最も有名ともいえる例が将棋です。強化学習により作成された将棋AIは、トッププロ以上の実力を保有するにいたっています。もはやプロがAIを上回る手を指すことが「AI超え」とニュースになってしまう状況です。
将棋のようなゲームの戦略を考えることが強化学習の得意分野であり、将棋と似ている囲碁はもちろん、昔に流行したインベーダーゲームやパックマンのようなゲームをクリアすることも可能です。
さらに、物理的なロボットに歩行などの運動を学習させることも可能です。ともするとあなたもロボットが走ったりバク転をする映像を見たことがあるのではないでしょうか? これらも強化学習により実現されています。
このように、強化学習は直接的に私たちの生活に役立つ技術なのです。
強化学習の簡単な説明と行動に焦点を当てたQ学習
将棋やインベーダーゲームに勝つ・クリアできるということは、そのときどきに応じて最適な行動を取ることができるということです。どんな状態においても、最適な行動がわかっていれば、当然ながらゲームを攻略できるのです。
今からPythonにより実装するのは、まさにこの「行動」に焦点を当てたQ学習というものです。Q学習は、各状態における行動の価値を算出します。そして各状態における行動の価値がわかれば、常に価値の高い行動を選択することで目的を達成することができるのです。
Q学習で使うたった一つの数式
強化学習において行動に焦点を当てたQ学習を実装する際に、一つだけ数式が必要となります。それが以下のようなものです。初めて見ると面食らうかもしれません。
\(Q(s_t,a_t)←(1−α)Q(s_t,a_t)+α(r_{t+1}+γmax_{a_{t+1}}Q(s_{t+1},a_{t+1}))\)
これは、行動の価値を計算するための数式になります。数式を見るだけで吐き気がする人は、以下の数式の導出と説明を省略して次節のPythonによる実装例に向かってもかまいません。以下では厳密な説明ではなく直感的に理解できる説明をします。
数式の導出と説明※このセクションは数式に興味がある人だけ読んでください
ここで、\(Q\)は行動の価値、\(t\)は時刻、\(s_t\)は時刻tの状態、\(a_t\)はそのときの行動です。つまり、\(Q(s_t,a_t)\)は時刻tにおける状態sのときの、aという行動の価値となります。とにかく、Qが行動の価値だとわかればOKです。
また、\(α\)(アルファ)は学習率、\(γ\)(ガンマ)は割引率となります。アルファは1回の学習の効率にかかわり、アルファが大きいほど行動価値を1回の学習で大きく変化させることになります。
ガンマは将来の報酬・利益を割り引くために用います(後で詳述)。わかりやすくいうと、今手元にある100円と、1年後に手に入る100円では1年後の100円の方が価値が低いということです。同じ100円なら、今すぐ手に入る方がよいですよね。たとえば割引率ガンマ=0.9のとき、1年後の100円の価値は100×0.9=90円となります。2年後の100円なら100×0.9×0.9=81円です。ガンマを設定することで、遅く手に入る利益ほど価値を低くします。
最後に、\(r\)というのは獲得できる報酬・利益のことです。
行動価値を計算するための上記数式を算出するためには、まず状態の価値(状態価値)を求める数式を考えるとわかりやすいです。状態価値を\(V(s_t)\)とすると、報酬・利益の\(r\)と\(γ\)(ガンマ)を用いて以下のようにできます。さきほどと同様、遠い将来の報酬・利益ほど割引が大きくなるのがポイントです。
\(V(s_t)= r_{t+1}+γr_{t+2}+γ^2r_{t+3}+γ^3r_{t+4}+・・・\)
どういうことかというと、その時点での状態価値は、将来得られる利益を現在まで割引したものの総和に等しいということです。
右辺第2項を変形すると
\(V(s_t)= r_{t+1}+γ(r_{t+2}+γr_{t+3}+γ^2r_{t+4}・・・)\)
すると、この式は以下のように書けることになります。
\(V(s_t)= r_{t+1}+γV(s_{t+1})\)
これをベルマン方程式と呼びます。状態価値に関してベルマン方程式が成り立つのと同様に、行動価値に関してもベルマン方程式が成り立ちます。
\(Q(s_t,a_t)= r_{t+1}+γQ(s_{t+1},a_{t+1})\)
この行動価値のベルマン方程式の左辺を右辺に移動させると、
\(0= r_{t+1}+γQ(s_{t+1},a_{t+1})-Q(s_t,a_t)(=TD誤差)\)
となるはずです。この右辺のことをTD誤差(Temporal difference error)と呼びます。理想的な状況ではTD誤差は0になるはずなのですが、学習が進んでない段階では0とはなりません。なぜなら学習の初期段階では\(Q(s_t,a_t)\)が初期値に依存したデタラメな値だからです。つまり、TD誤差がゼロとなること、言い換えるとベルマン方程式が成り立つよう行動価値Qを学習することが目的となります。
そして、\(α\)を学習率として以下のように\(Q(s_t,a_t)\)を更新し、正しい値に近づけていきます。
\(Q(s_t,a_t)←Q(s_t,a_t)+αTD誤差\)
つまり、TD誤差が0より大きいときはTD誤差を0に近づけるため\(Q(s_t,a_t)\)を少し大きくし、TD誤差が0より小さいときはTD誤差を0に近づけるため\(Q(s_t,a_t)\)を少し小さくする、という試行錯誤を繰り返し行うことに等しいです。このように価値更新をする方法をSARSA法といいます。
Q学習は、価値更新の際にSARSA法のTD誤差を少し変えるだけです。
\(TD誤差 = r_{t+1}+γQ(s_{t+1},a_{t+1})-Q(s_t,a_t)\)
だったものを、
\(TD誤差 = r_{t+1}+γmax_{a_{t+1}}Q(s_{t+1},a_{t+1})-Q(s_t,a_t)\)
に変えます。そのため、Q学習は、常に最も価値の高い行動によって価値更新を行うことになります。
したがって、Q学習の数式は、以下のようになります。
\(Q(s_t,a_t)←Q(s_t,a_t)+α(r_{t+1}+γmax_{a_{t+1}}Q(s_{t+1},a_{t+1})-Q(s_t,a_t))\)
右辺を式変形すれば、最終的に以前示した「1つだけ使う数式」が得られます。
\(Q(s_t,a_t)←(1−α)Q(s_t,a_t)+α(r_{t+1}+γmax_{a_{t+1}}Q(s_{t+1},a_{t+1}))\)
この式を見ると\(α\)の学習率という意味合いがわかります。\(α\)が0に近いほど、価値更新の際に現時点の行動価値が強く反映されます。そのため価値の更新がゆるやかに行われていくことになります。逆に\(α\)が1に近いほど、行動価値が大きく変わっていきます。だから学習率なのです。
以上がざっくりとしたQ学習の数学的背景となります。結局使うのは
\(Q(s_t,a_t)←(1−α)Q(s_t,a_t)+α(r_{t+1}+γmax_{a_{t+1}}Q(s_{t+1},a_{t+1}))\)
だけとなります。
PythonでQ学習という強化学習を実装し、迷路を解く(最短ルートを見つける)
コードをシンプルにするため、以下のような非常に簡単な迷路を考えます。
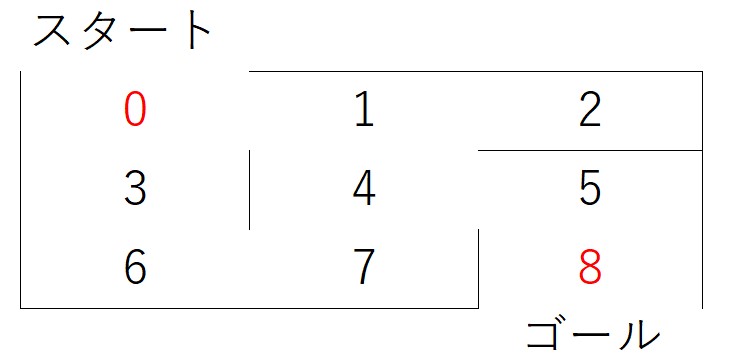
0からスタートしてゴールの8に最短経路で行くことが目的です。これぐらいの迷路なら人間なら簡単です。0→1→4→5→8が最短経路ですよね。これをQ学習という強化学習により求めます。さらに、スタート地点を自由に選んでゴール(8)への最短経路を求めることができるようにしました。
コードに詳しい説明をつけましたので、そのコードを見ると何をしているかが理解できるはずです。説明が邪魔でコードが見にくい場合は、コピー&ペーストをして適宜説明を削除してください。
#必要なモジュールをインポート
import numpy as np
gamma = 0.9#将来価値の割引。小さいほど行動直後の利益を重視。また、この割引率の存在が効率的な学習の鍵となる。
alpha = 0.1#学習率。大きいと1回の学習による値の更新が急激となる。小さいほど更新がゆるやかとなる。後で詳述。
#報酬の設定
#各場所から移動できる箇所に報酬1を与え、それ以外を0とすることで移動できる方向を指示
#以下の行列の各行が場所に対応。0行目は迷路の位置0、1行目が迷路の位置1
#ゴールとなる8の報酬を大きく設定する
reward = np.array([[0,1,0,1,0,0,0,0,0],#0から1,3に移動できるので、そこに1
[1,0,1,0,1,0,0,0,0],#1から0,2,4に移動できるので、そこに1
[0,1,0,0,0,0,0,0,0],
[1,0,0,0,0,0,1,0,0],
[0,1,0,0,0,1,0,1,0],
[0,0,0,0,1,0,0,0,10000],#8をゴールより5→8の報酬を大きく
[0,0,0,1,0,0,0,1,0],
[0,0,0,0,1,0,1,0,0],
[0,0,0,0,0,1,0,0,0]])
#Q値(行動価値)の初期値を設定。今回は0を初期値とする。
Q = np.array(np.zeros([9,9]))
#Q学習を実装し、各位置における行動価値を算出
#以下の学習を実行すると、行動価値Qを求められる。Qの各行が位置に対応し、たとえば0行1列目の値は0から1に移動する行動の価値となる。
#p_stateのpはpresent(現在)、n_state,n_actionsのnはnext(次)のn
for i in range(10000):#1万回繰り返し学習を行う
p_state = np.random.randint(0,9)#現在の状態をランダムに選択
n_actions = []#次の行動の候補を入れる箱
for j in range(9):
if reward[p_state,j] >= 1:#rewardの各行が1以上のインデックスを取得
n_actions.append(j)#これでp_stateの状態で移動できる場所を取得
n_state = np.random.choice(n_actions)#行動可能選択肢からランダムに選択
#Q値の更新。学習率が小さいほど現在の行動価値が重視され、更新がゆるやかとなる
#ここでQ学習に用いる「たった一つの数式」を利用して行動価値を学習していく
Q[p_state,n_state] = (1-alpha)*Q[p_state,n_state]+alpha*(reward[p_state,n_state]+gamma*Q[n_state,np.argmax(Q[n_state,])])
#最短ルート表示関数の定義。Q値が最も高い行動をappendで追加しているだけ
def shortest_path(start):#0~8の数字を入力。好きなところからスタート可能
path = [start]#pathに経路を追加していく
p_pos = start#p_posは現在位置(positionの略)
n_pos = p_pos#n_pos(次の位置)にいったんp_posを代入
while(n_pos != 8):#n_posがゴール(8)になるまで繰り返し行動を選択
n_pos = np.argmax(Q[p_pos,])#各位置の行動価値が最も高い行動を選択
path.append(n_pos)#経路をpathに追加
p_pos = n_pos#行動後が次のp_posとなる
return path
print(shortest_path(0))#スタートを0として最短経路を表示
以上のコードを実行すると、たしかに0からスタートしたときの最短経路が[0,1,4,5,8]となりました。
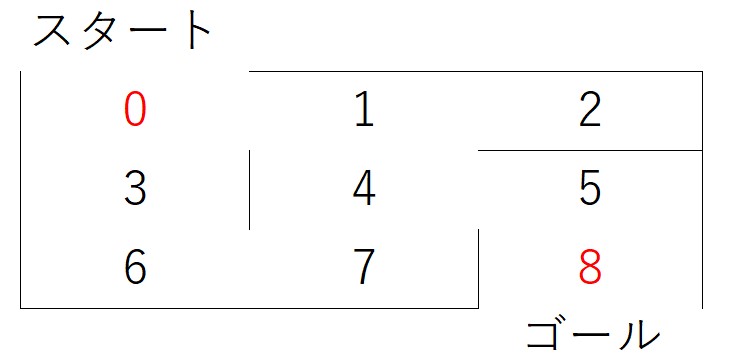
print(shortest_path(6))
とすると[6,7,4,5,8]となり、やはり6からスタートしたときの最短経路となりましたね。
なぜQ学習で最短経路を求められるのか
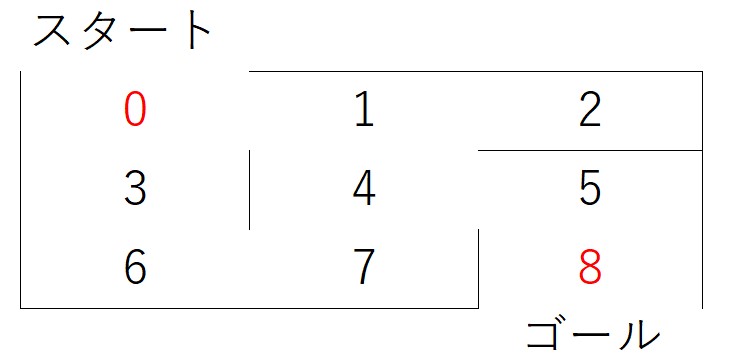
最短経路となることには、割引率を設定していることが大きく関わっています。
0から1への移動したとき、5→8の大きな報酬を得るまでには少なくともあと3回行動する必要があります。
0から3への移動したとき、5→8の大きな報酬を得るまでには少なくともあと5回行動する必要があります。
つまり、0から3への移動の場合、5→8の大きな報酬に掛け算される割引率が2回多くなってしまうのです。
割引率が多く掛け算されるほど値は小さくなります。
たとえば、
\(10000×0.9^4=6561\)
\(10000×0.9^5=5904.9\)
したがって、ゴールの8に近い0~1への移動の方が行動価値が高くなり、かつ最短経路になっているということです。
まとめ
ということで、迷路の最短経路を導くAIを作成できました。今回は非常に単純な迷路でQ学習を実装しましたが、迷路が複雑になっても上記コードを拡張するだけで難解な迷路を解くことができます。ぜひあなたもオリジナルの迷路を作成し、上記コードを一部変更して迷路を解いてみてください。今回の記事を通して、強化学習の雰囲気をご理解いただけたのではないでしょうか? 強化学習は、非常に面白いですよね!
ここまで長文を読んでいただきありがとうございました。そして、お疲れさまでした!またお会いしましょう!