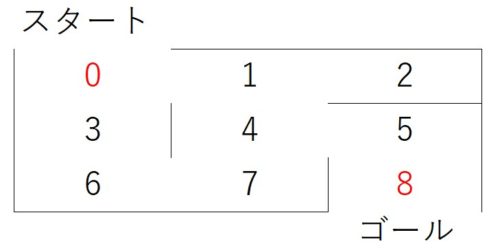遺伝的アルゴリズム(Genetic Algorithms:略してGAとも呼ぶ)とは、生物の進化の過程を模倣した強力な解探索アルゴリズムです。なぜ解探索アルゴリズムが必要かというと、数式などで厳密に解くことができない問題に対して、試行錯誤により近似解を提供してくれるからです。
遺伝的アルゴリズムは、ナップサック問題や巡回セールスマン問題など、厳密に解こうとする(解を全探索しようとする)とスーパーコンピューターで膨大な計算時間が必要となる問題を、現実的な時間で解くことを可能にします。
この記事では、遺伝アルゴリズムの概要を説明し、PythonのDEAPライブラリを用いて簡単な最大・最小化問題とナップサック問題を解くPythonコード実装例を紹介します。Pythonコードのイメージをつかんでもらうため、非常に簡単な例題をあえて解くことにします。これまでDEAPを難しいと思っていた人でも概要を理解いただけるのではと思います。
目次
ナップサック問題とは?
ナップサック問題は、以下のような非常に簡単そうに思える問題ですが、実は厳密に解を見つけようとすると非常に困難であることが知られています。
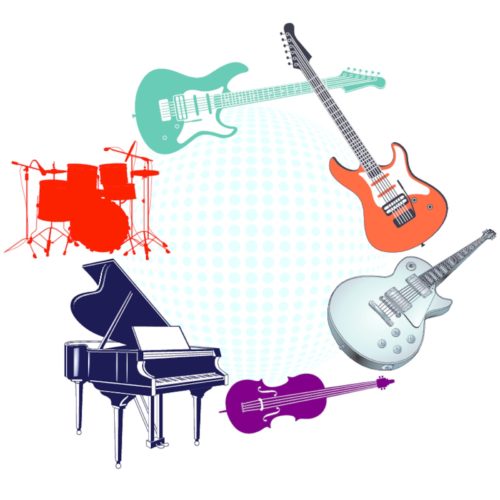
容量100のナップサックに下図の品物を詰め込む。このとき、詰め込んだ品物の総価値を最大化するには、何をいくつ詰め込むとよいか? ただし、同じ品物を何個詰め込んでもよい。

非常に簡単そうに思いますよね?
巡回セールスマン問題
以下の問題は巡回セールスマン問題として知られており、意外にも解を求めることが困難だとわかっています。
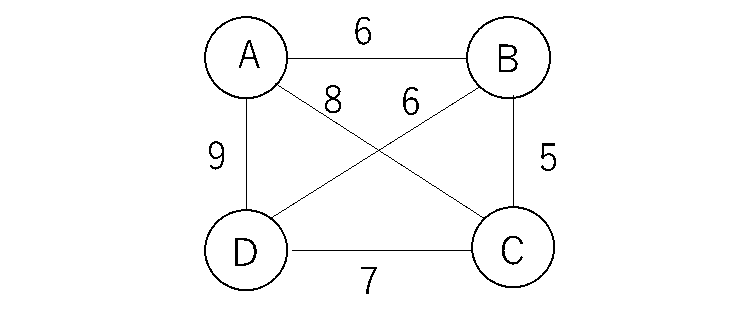
下図は、都市A,B,C,Dの距離関係を表している。ある都市から出発し、すべての都市を訪問し、出発点に戻るには、どのような順番で都市を回ると最短経路となるか?
遺伝的アルゴリズムのモチーフであるダーウィンの進化論
遺伝的アルゴリズムのモチーフはダーウィンの進化論です。概要としては、「さまざまな生物がいる地球では、環境に適応した優秀な生物だけが子孫を残し、劣った生物は淘汰される。ときに、生物は突然変異を起こすことがあり、前の世代よりも優秀になったり劣ったりすることもある。こうした繰り返しにより、生物は進化してきた」のような具合です。遺伝的アルゴリズムは、優秀な生物 = 優れた解答とみなします。生物の遺伝機構を比較的忠実にモデル化していますので、まずは以下のように言葉を言い換えます。
・生物→個体、染色体(解)
・生存能力→適応度(評価関数で解を評価)
・生殖行動→交叉
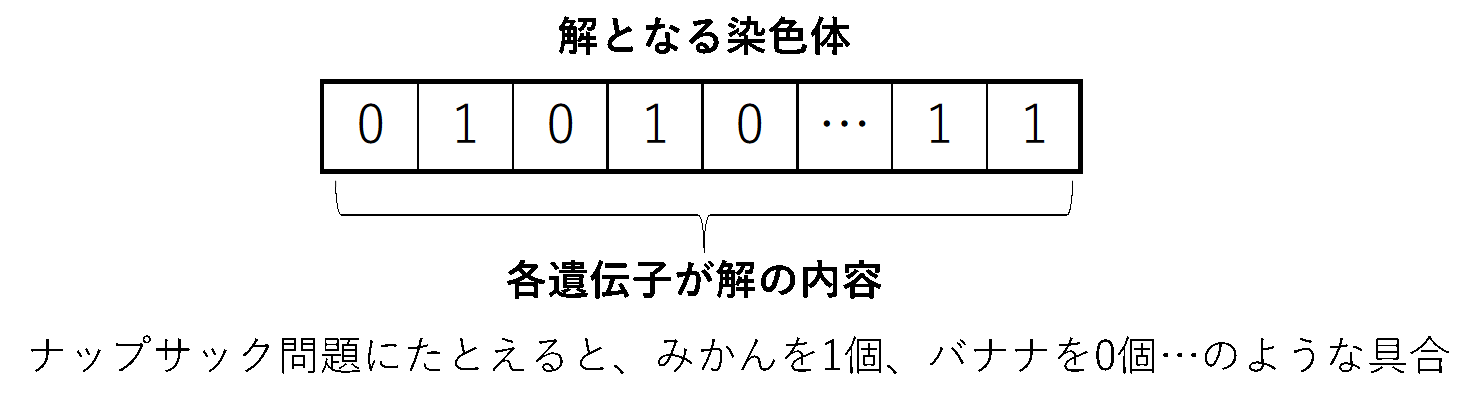
遺伝的アルゴリズムでは、下図のように解を染色体(遺伝子の組)という形で表現します。
遺伝的アルゴリズムの手順
遺伝的アルゴリズムの手順は次のようになります。
①初期集団の生成
※終了条件を満たすまで、以下の②~⑤をループ
②適応度の評価
③選択
④交叉
⑤突然変異
①初期集団の生成
まずは1つの世代を構成する個体数を決め、染色体をランダムに生成。
②適応度の評価
あらかじめ決めた評価関数で染色体を評価します。ナップサック問題なら評価関数は、「おにぎりの数×価値+ポテトチップスの数×価値+・・・」のようになります。
③選択
次世代に子を残す親となる個体を選択します。これにはルーレットやトーナメントという選択手法がよく利用され、適応度が高い個体ほど選択される確率が高くなるようにします。つまり、次世代の個体は前世代で適応度の高かった個体の遺伝子を受け継ぐものが多くなるということです。併せて、エリート保存戦略も用いられます。これは最も適応度の高い個体をそのまま次世代に複製する方法で、その時点で最も良い解が選択や突然変異で消えないというメリットがあります。
④交叉
親それぞれの遺伝子を引き継ぐ子を作成します。これには、一点交叉や多点交叉、ブレンド交叉などさまざまな交叉手法があります。

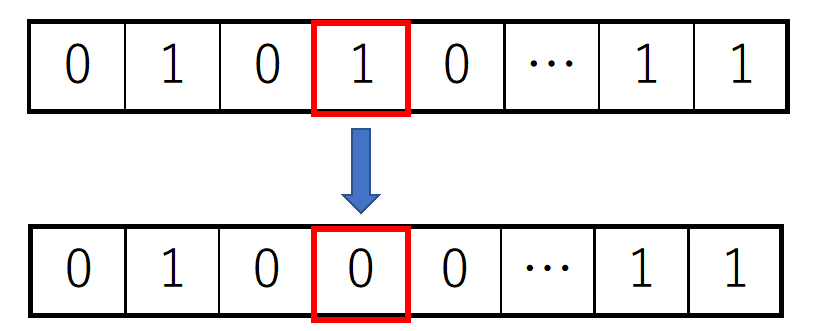
⑤突然変異
交叉だけでは、個体の親に依存するような限られた子しか生成することができません。突然変異は、染色体上の遺伝子を他の遺伝子に置き換えます。これにより交叉だけでは生成できない子を生成し、個体群の多様性を維持することができます。数学的には、局所最適解(本当の最適解ではない偽の最適解)に陥る確率を減らす役割があります。
以上の操作を、終了条件を満たすまで繰り返し、最適解を探索するのです。これは、機械学習が損失関数を最小化する重みを探索する過程と似ていますよね。
Pythonライブラリによる遺伝的アルゴリズムの実装
Pythonで遺伝的アルゴリズムを実装するには、DEAPというライブラリを用いることが多いです。Pyevolveというライブラリの方が簡単そうに思えたのですが、開発が相当昔に止まっているようです。
DEAPの導入は、通常通り以下のコマンドで行なえます。
pip install deap
DEAPライブラリによる最小化問題の実装例
今回は、\((x-1)^2 + (y-2)^2\)という簡単な関数の最小値を与える\(x,y\)求めることにします。2乗足す2乗となっていますので、0以上であることは間違いなく、\(x=1,y=2\)のときが最小値0となりますよね。遺伝的アルゴリズムを使うまでもない簡単な問題ですが、これを遺伝的アルゴリズムで解くことでライブラリの使い方などを効率的に学べます。
コメントに詳細な解説をつけましたので、そちらを見ていただくと何をやっているかを理解していただけると思います。始めてコードを見ると面食らうかもしれませんが、よく眺めてみるとおおよその使い方がわかるはずです。
#個体の各遺伝子を決めるために使用
import random
#DEAPの中にある必要なモジュールをインポート
from deap import base
from deap import creator
from deap import tools
from deap import algorithms
#最小化問題として設定(-1.0で最小化、1.0で最大化問題)
#面食らうかもしれませんが、目的が最小化の場合は以下のように設定します。
creator.create("FitnessMin", base.Fitness, weights=(-1.0,))
#個体の定義(list型と指定しただけで、中身の遺伝子は後で入れる)
#これも面食らうかもしれませんが、個体を準備したと思ってください。
creator.create("Individual", list, fitness=creator.FitnessMin)
#目的関数の定義。必ずreturnの後に,をつける
def obfunc(individual):
x = individual[0]
y = individual[1]
object = (x-1)**2 + (y-2)**2
#(x,y)=(1,2)で最小になるはず。これを遺伝的アルゴリズムで求める
return object,
#各種関数の設定を行います
#交叉、選択、突然変異などには、DEAPのToolbox内にある関数を利用
toolbox = base.Toolbox()
#random.uniformの別名をattribute関数として設定。各個体の遺伝子の中身を決める関数(各遺伝子は-50~50のランダムな値)
toolbox.register("attribute", random.uniform, -50,50)
#individualという関数を設定。それぞれの個体に含まれる2個の遺伝子をattributeにより決めるよ、ということ。
toolbox.register("individual", tools.initRepeat, creator.Individual, toolbox.attribute, 2)
#集団の個体数を設定するための関数を準備
toolbox.register("population", tools.initRepeat, list, toolbox.individual)
#トーナメント方式で次世代に子を残す親を選択(tornsizeは各トーナメントに参加する個体の数)
toolbox.register("select", tools.selTournament, tournsize=5)
#交叉関数の設定。ブレンド交叉という手法を採用
toolbox.register("mate", tools.cxBlend,alpha=0.2)
#突然変異関数の設定。indpbは各遺伝子が突然変異を起こす確率。muとsigmaは変異の平均と標準偏差
toolbox.register("mutate", tools.mutGaussian, mu=[0.0, 0.0], sigma=[20.0, 20.0], indpb=0.2)
#評価したい関数の設定(目的関数のこと)
toolbox.register("evaluate", obfunc)
#以下でパラメータの設定
#今回は最も単純な遺伝的アルゴリズムの手法を採用
#乱数を固定
random.seed(64)
#何世代まで行うか
NGEN = 50
#集団の個体数
POP = 80
#交叉確率
CXPB = 0.9
#個体が突然変異を起こす確率
MUTPB = 0.1
#集団は80個体という情報の設定
pop = toolbox.population(n=POP)
#集団内の個体それぞれの適応度(目的関数の値)を計算
for individual in pop:
individual.fitness.values = toolbox.evaluate(individual)
#パレート曲線上の個体(つまり、良い結果の個体)をhofという変数に格納
hof = tools.ParetoFront()
#今回は最も単純なSimple GAという進化戦略を採用
algorithms.eaSimple(pop, toolbox, cxpb=CXPB, mutpb=MUTPB, ngen=NGEN, halloffame=hof)
#最終的な集団(pop)からベストな個体を1体選出する関数
best_ind = tools.selBest(pop, 1)[0]
#結果表示
print("最も良い個体は %sで、そのときの目的関数の値は %s" % (best_ind, best_ind.fitness.values))
上記コードを実行すると、以下が表示されます。
「最も良い個体は [0.9999999999999998, 2.0]で、そのときの目的関数の値は (4.930380657631324e-32,)」
ということで、\((x,y)=(1,2)\)に非常に近い近似解を得られましたね。まずは非常に簡単な関数の最小化問題を解きました。
DEAPライブラリによるナップサック問題の実装例
さきほども紹介した以下のナップサック問題をDEAPライブラリを使用して解いてみたいと思います。ナップサック問題は最大化問題としてコードを組みます。
容量100のナップサックに下図の品物を詰め込む。このとき、詰め込んだ品物の総価値を最大化するには、何をいくつ詰め込むとよいか? ただし、同じ品物を何個詰め込んでもよい。

各個体は(1,4,0,2,7,3)のように6個の遺伝子を持っており、(おにぎりの個数,ポテトチップスの個数,お茶の本数,コーヒーの本数,バナナの本数,パンの個数)となるように設定します。ただ、今回の問題は非常に単純であるため、コーヒーのコスパが良さそうなことがひと目でわかります。コーヒー20本のときが最も価値が高そうですね。以下はさきほどとほぼ同様のコードとなります。実はうまくいかないのですが、あえてやってみましょう。
#個体の各遺伝子を決めるために使用
import random
#DEAPの中にある必要なモジュールをインポート
from deap import base
from deap import creator
from deap import tools
from deap import algorithms
#最大化問題として設定
creator.create( "FitnessMax", base.Fitness, weights=(1.0,) )
#個体の定義(list型と指定しただけで、中身の遺伝子は後で入れる)
creator.create("Individual", list, fitness = creator.FitnessMax )
#各品物の(重さ,価値)をitemsに格納
items = {}
items[0]=(5,110)
items[1]=(10,140)
items[2]=(9,150)
items[3]=(5,130)
items[4]=(5,110)
items[5]=(4,90)
#目的関数の定義。#必ずreturnの後に,をつける
#個体は(1,3,0,2,4,3)などであり、総価値と総重量を計算します。
#重量が100を超えてはいけないので、100を超えた場合、価値を0にします。
def evalKnapsack( individual ):
weight = 0.0
value = 0.0
for i in range(6):
weight += items[i][0]*individual[i]
value += items[i][1]*individual[i]
if weight > 100:
value=0.0
return value,
#各種関数の設定を行います
toolbox = base.Toolbox()
#random.uniformの別名をattribute関数として設定。各個体の遺伝子の中身を決める関数(各遺伝子は0~10のランダムな整数)
toolbox.register("attribute", random.randint, 0,10)
#individualという関数を設定。それぞれの個体に含まれる6個の遺伝子をattributeにより決めるよ、ということ。
toolbox.register("individual", tools.initRepeat, creator.Individual, toolbox.attribute, 6)
#集団の個体数を設定するための関数を準備
toolbox.register("population", tools.initRepeat, list, toolbox.individual)
#トーナメント方式で次世代に子を残す親を選択(tornsizeは各トーナメントに参加する個体の数)
toolbox.register("select", tools.selTournament, tournsize=5)
#交叉関数の設定。一点交叉を採用
toolbox.register("mate", tools.cxOnePoint)
#突然変異関数の設定。indpbは各遺伝子が突然変異を起こす確率。変異は0~20の整数で変異
toolbox.register("mutate", tools.mutUniformInt,low=0,up=20,indpb=0.2)
#評価したい関数の設定(目的関数のこと)
toolbox.register("evaluate", evalKnapsack)
#乱数の固定
random.seed(128)
#何世代まで行うか
NGEN = 50
#集団の個体数
POP = 80
#交叉確率
CXPB = 0.9
#個体が突然変異を起こす確率
MUTPB = 0.1
#集団は80個体という情報の設定
pop = toolbox.population(n=POP)
#集団内の個体それぞれの適応度(目的関数の値)を計算
for ind in pop:
ind.fitness.values = toolbox.evaluate(ind)
#パレート曲線上の個体(つまり、良い結果の個体)をhofという変数に格納
hof = tools.ParetoFront()
#最も単純なSimple GAという進化戦略を採用
algorithms.eaSimple(pop, toolbox, cxpb=CXPB, mutpb=MUTPB, ngen=NGEN, halloffame=hof)
#最終的な集団(pop)からベストな個体を1体選出する関数
best_ind = tools.selBest(pop, 1)[0]
#結果表示
print("最も良い個体は %sで、そのときの目的関数の値は %s" % (best_ind, best_ind.fitness.values))
コードを実行すると、「最も良い個体は [5, 0, 0, 9, 2, 5]で、そのときの目的関数の値は (2390.0,)」となりました。つまり、おにぎり5個、コーヒー9本、バナナ2本、パン5個がベストとなりました。総価値は2390です。つまり、コーヒー20本とはなりませんでした。
ここで、コードの集団の個体数POPを極端ですが以下のように80から15000に変更します。集団の個体数80では少なすぎてベストな答えにたどりつくのは難しそうです。
#集団の個体数 POP = 15000
上記のように変更したコードを実行すると、「最も良い個体は [0, 0, 0, 20, 0, 0]で、そのときの目的関数の値は (2600.0,)」となり、たしかにベストの解となりました。流れのわかりやすさを優先して上記のようなコードにしましたが、DEAPライブラリのナップサック問題チュートリアルのように目的関数などを設定した方が良いと思われます。興味のある方はぜひ挑戦してみてください。
ただ、遺伝的アルゴリズムの面白さとDEAPライブラリの使用イメージを理解いただけたのではないでしょうか? ここまで長文を読んでいただきありがとうございました。そして、お疲れさまでした!またお会いしましょう!